Kompetensi
Pengantar
gaya F1= 20 N dengan x1=-1m
gaya F2=30 N dengan x2=1m
gaya F3=40 N dengan x3=2m
gaya F4= 10 N dengan x4=3m
Letak Resultan keempat gaya tersebut dapat di tentukan dengan persamaan
Nah setelah mempelajari bagaimana mencari letak resultan gaya sejajar yang bekerja pada benda marilah kita lihat bagaimana letak resultan gaya yang bekerja pada sebuah benda homogen berbentuk tak beraturan berikut ini.
w1= w2= w3= berat masing-masing partikel
X1 = letak partikel 1 pada sumbu x
X2 = letak partikel 2 pada sumbu x
X3 = letak partikel 3 pada sumbu x
y1 = letak partikel 1 pada sumbu y
y2 = letak partikel 2 pada sumbu y
y3 = letak partikel 3 pada sumbu y
z1 = letak partikel 1 pada sumbu z
z2 = letak partikel 2 pada sumbu z
z3 = letak partikel 3 pada sumbu z
Hal-hal Istimewa Pada Titik Berat
Hal-hal Istimewa Pada Titik Berat
a. Titik berat benda homogen satu dimensi (garis)
l1 = panjang garis 1
l2 = panjang garis 2
Bentuk benda homogen berbentuk garis (1 dimensi) dan letak titik beratnya.
Contoh soal :
Tentukanlah letak titik berat benda homogen satu dimensi seperti gambar berikut ini!
b. Titik berat benda-benda homogen berbentuk luasan (dua dimensi)
A1 = Luas Bidang 1
A2 = Luas bidang 2
x1 = absis titik berat benda 1
x2 = absis titik berat benda 2
y1 = ordinat titik berat benda 1
y2 = ordinat titik berat benda 2
Contoh soal:
Sebuah karton berbentu huruf L dengan ukuran seperti pada gambar di bawah.
Tentukan koordinat titik berat karton tersebut!
c. Titik berat benda-benda homogen berdimensi tiga
V1=Volume Benda 1
V2= Volume Benda 2
x1 = absis titik berat benda 1
x2 = absis titik berat benda 2
y1 = ordinat titik berat benda 1
y2 = ordinat titik berat benda 2
- Siswa dapat menjelaskan konsep titik berat
- Siswa dapat menentukan letak titik berat dari susunan dua benda atau lebih satu dimensi (panjang)
- Siswa dapat menentukan letak titik berat dari susunan dua benda atau lebih dua dimensi (bidang)
- Siswa dapat menentukan letak titik berat dari susunan dua benda atau lebih tiga dimensi (ruang)
Pengantar
Pernahkah kamu melihat permainan sirkus seperti gambar di atas..?
Apakah rahasia dari para pemain sirkus sehingga dapat beraksi seperti gambar di atas tanpa jatuh..?
Rahasianya adalah titik berat. Apakah titik berat itu? Mari kita cari tahu..!
Konsep Titik Berat Apakah rahasia dari para pemain sirkus sehingga dapat beraksi seperti gambar di atas tanpa jatuh..?
Rahasianya adalah titik berat. Apakah titik berat itu? Mari kita cari tahu..!
Semua benda di bumi mempunyai berat. Berat suatu benda dapat dianggap terkonsentrasi pada satu titik yang di sebut pusat gravitasi atau titik berat. Pada titik berat ini gaya-gaya yang bekerja menghasilkan momen resultan sama dengan nol. Karena itulah benda yang di tumpu pada titik beratnya akan berada dalam keseimbangan statik. Dengan kata lain titik berat adalah titik tangkap dari semua gaya yang bekerja. Contoh berikut ini menunjukkan bagaimana menentukan letak resultan gaya yang sejajar.
Contoh soal
Empat buah gaya masing-masing F1 = 20N, F2 = 30N, F3 = 40N dan F4 = 10N bekerja pada sepanjang sumbu x seperti gambar berikut. Tentukanlah letak resultan keempat gaya tersebut!
Jawab:Empat buah gaya masing-masing F1 = 20N, F2 = 30N, F3 = 40N dan F4 = 10N bekerja pada sepanjang sumbu x seperti gambar berikut. Tentukanlah letak resultan keempat gaya tersebut!
gaya F1= 20 N dengan x1=-1m
gaya F2=30 N dengan x2=1m
gaya F3=40 N dengan x3=2m
gaya F4= 10 N dengan x4=3m
Letak Resultan keempat gaya tersebut dapat di tentukan dengan persamaan
Nah setelah mempelajari bagaimana mencari letak resultan gaya sejajar yang bekerja pada benda marilah kita lihat bagaimana letak resultan gaya yang bekerja pada sebuah benda homogen berbentuk tak beraturan berikut ini.
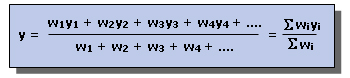
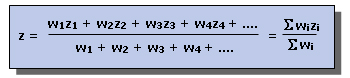
Benda dengan berat w tersusun atas partikel-partikel dengan berat w1, w2, w3, .... yang terletak pada koordinat (x1,y2,z3), (x2,y2,z2), (x3,y3,z3) dan seterusnya...
letak titik resultan gaya-gaya tersebut secara umum dapat ditentukan dengan persamaan w1= w2= w3= berat masing-masing partikel
X1 = letak partikel 1 pada sumbu x
X2 = letak partikel 2 pada sumbu x
X3 = letak partikel 3 pada sumbu x
y1 = letak partikel 1 pada sumbu y
y2 = letak partikel 2 pada sumbu y
y3 = letak partikel 3 pada sumbu y
z1 = letak partikel 1 pada sumbu z
z2 = letak partikel 2 pada sumbu z
z3 = letak partikel 3 pada sumbu z
Hal-hal Istimewa Pada Titik Berat
Hal-hal Istimewa Pada Titik Berat
a. Titik berat benda homogen satu dimensi (garis)
Untuk benda-benda berbentuk memanjang seperti kawat , massa benda dianggap diwakili oleh panjangnya (satu dimensi) dan titik beratnya dapat dinyatakan dengan persamaan berikut:
l1 = panjang garis 1
l2 = panjang garis 2
Bentuk benda homogen berbentuk garis (1 dimensi) dan letak titik beratnya.
Contoh soal :
Tentukanlah letak titik berat benda homogen satu dimensi seperti gambar berikut ini!
b. Titik berat benda-benda homogen berbentuk luasan (dua dimensi)
Jika tebal diabaikan maka benda dapat dianggap berbentuk luasan (dua dimensi), dan titik berat gabungan benda homogen berbentuk luasan dapat ditentukan dengan persamaan berikut:
A1 = Luas Bidang 1
A2 = Luas bidang 2
x1 = absis titik berat benda 1
x2 = absis titik berat benda 2
y1 = ordinat titik berat benda 1
y2 = ordinat titik berat benda 2
Titik berat benda homogen berbentuk luasan yang bentuknya teratur terletak pada sumbu simetrinya. Untuk bidang segi empat, titik berat diperpotongan diagonalnya, dan untuk lingkaran terletak dipusat lingkaran. Titik berat bidang homegen di perlihatkan pada tabel berikut:
Sebuah karton berbentu huruf L dengan ukuran seperti pada gambar di bawah.
Tentukan koordinat titik berat karton tersebut!
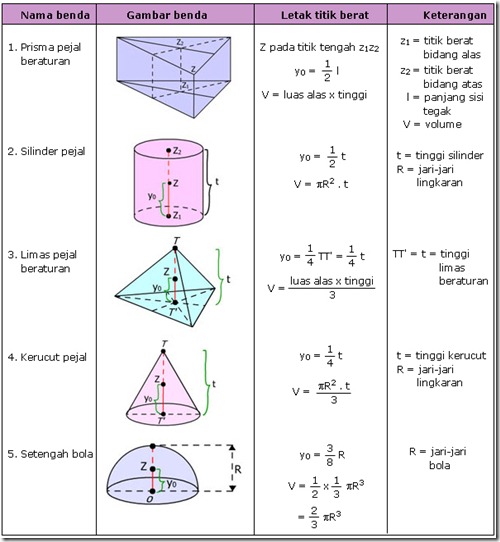
c. Titik berat benda-benda homogen berdimensi tiga
Letak titik berat dari gabungan beberapa benda pejal homogen berdimensi tiga dapat ditentukan dengan persamaan:
V1=Volume Benda 1
V2= Volume Benda 2
x1 = absis titik berat benda 1
x2 = absis titik berat benda 2
y1 = ordinat titik berat benda 1
y2 = ordinat titik berat benda 2