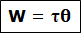Kompetensi
Indikator
- Siswa dapat mendefinisikan gerak rotasi benda tegar
- Siswa dapat menghitung besaran-besaran yang ada pada gerak rotasi benda tegar
- Siswa dapat menghitung besarnya momen gaya pada suatu benda yang berotasi benda tegar
- Siswa dapat menghitung besarnya momen inersia suatu sistem partikel yang berotasi
- Siswa dapat menghitung besarnya momen inersia suatu benda tegar berotasi
- Siswa dapat menghitung besarnya energi kinetik rotasi benda tegar
- Siswa dapat menghitung besarnya momentum sudut suatu benda berotasi benda tegar
- Siswa dapat menghitung besaran-besaran yang ada pada benda yang bergerak menggelinding
Materi
Pendahuluan
Alat apa yang digunakan oleh tukang bangunan saat memindahkan pasir, bata atau material yang lain dari satu tempat ke tempat yang lain?
Alat apa yang digunakan oleh tukang tambal ban saat membuka ban sebuah mobil ?
Pernahkah kalian bermain dengan yoyo? Apa yang terjadi saat yoyo tersebut meluncur ke bawah ?
Bagaimana dengan katrol?
Kalian akan dapat menjawab pertanyaan tersebut setelah mempelajari beberapa materi berikut ini, yaitu:
Pernahkah kalian bermain dengan yoyo? Apa yang terjadi saat yoyo tersebut meluncur ke bawah ?
Bagaimana dengan katrol?
Kalian akan dapat menjawab pertanyaan tersebut setelah mempelajari beberapa materi berikut ini, yaitu:
- Gerak Rotasi Benda Tegar
- Momen Gaya
- Momen Inersia
- Energi Kinetik Rotasi Benda Tegar
- Hukum Kekekalan Momentum Sudut
- Gerak Menggelinding
Gerak Rotasi Benda Tegar
Gerak benda yang berputar terhadap suatu sumbu putar (poros) atau sumbu rotasi disebut gerak rotasi. Contoh gerak rotasi diantaranya: gerakan putaran bumi terhadap sumbunya, roda sepeda yang berputar, gerakan pintu yang berputar pada engselnya, dan masih banyak lagi. Perhatikan animasi berikut ini!
Gambar menunjukkan rotasi sebuah benda terhadap sumbu tetap
yang melalui O dan tegak lurus bidang gambar
Dengan menggunakan sistem koordinat polar, posisi benda dapat dinyatakan dalam r dan θ. Pada gambar dibuat hubungan bahwa:
komponen pada sumbu x ; x = r cos θ
komponen pada sumbu y ; y = r sin θ
besar posisi ;
komponen pada sumbu y ; y = r sin θ
besar posisi ;
arah posisinya ;
Keterangan:
r = jarak titik P terhadap titik pusat benda melingkar
x = proyeksi titik P terhadap sumbu x
y = proyeksi titik P terhadap sumbu y
θ = sudut r terhadap x
x = proyeksi titik P terhadap sumbu x
y = proyeksi titik P terhadap sumbu y
θ = sudut r terhadap x
Hubungan besaran-besaran s , r dan θ secara geometri adalah:
Jika θ dinyatakan dalam radian maka:
Keterangan :
s = panjang busur lingkaran dalam meter
r = jari-jari titik tinjauan terhadap pusat lingkaran dalam meter
θ = sudut yang dibentuk dalam radian (derajat)
s = panjang busur lingkaran dalam meter
r = jari-jari titik tinjauan terhadap pusat lingkaran dalam meter
θ = sudut yang dibentuk dalam radian (derajat)
Persamaan Gerak Rotasi Benda Tegar
Kecepatan Sudut
Dinotasikan dengan  , satuannya rad/s atau putaran/s.
, satuannya rad/s atau putaran/s.
Kecepatan sudut rata-rata partikel adalah perubahan posisi sudut dibagi selang waktu. Dengan persamaannya dirumuskan sebagai:
Keterangan:
∆θ = θ2 – θ1 = perubahan posisi sudut dalam rad atau putaran
∆t = t2 – t1 = selang waktu dalam sekon
∆t = t2 – t1 = selang waktu dalam sekon
Kecepatan sudut sesaat
Dinotasikan dengan ω, satuannya rad/s atau putaran/s.
Untuk Δθ yang diambil kecil sekali (mendekati nol) maka kecepatan sudut rata-ratanya merupakan gradien garis singgung kurva posisi sudut terhadap waktu. Kecepatan sudut tersebut dinamakan kecepatan sudut sesaat. Secara matematis kecepatan sudut rata-rata dituliskan sebagai:
Keterangan:
ω = kecepatan sudut (radian /sekon) atau dengan satuan lain yaitu rpm (rotation perminute)
Hubungan timbal balik posisi sudut dari kecepatan sudut
Posisi sudut didapat dari kecepatan sudutnya dengan cara mengintegralkan kecepatan sudut.
Apabila posisi sudut awal partikel (t=0) adalah θ0, maka posisi sudut pada waktu t dapat dicari dengan persamaan sebagai berikut:
ω = 
Dengan menggunakan integral biasa dapat ditulis hubungan antara posisi sudut dari kecepatan sudut sebagai berikut:Keterangan:
θ0 = posisi sudut awal, satuannya radian
θt = posisi sudut setelah t sekon, satuannya radian
t = lamanya berputar, satuannya sekon
ω = kecepatan sudut, satuannya radian/sekon
Percepatan sudut rata-rata
Dinotasikan dengan  , satuannya rad/s2 atau putaran/s2.
, satuannya rad/s2 atau putaran/s2.
Percepatan sudut rata-rata dapat didefinisikan sebagai perubahan kecepatan sudut dibagi selang waktunya.
Keterangan:
∆ω = ω2 – ω1 = perubahan kecepatan sudut dalam rad/s
∆t = t2 – t1 = selang waktu dalam sekon
∆t = t2 – t1 = selang waktu dalam sekon
Percepatan sudut sesaat
Dinotasikan dengan , satuannya rad/s2 atau putaran/s2
, satuannya rad/s2 atau putaran/s2
Untuk Δt yang kecil (mendekati nol) maka percepatan sudut rata-rata merupakan gradien garis singgung kurva kecepatan sudut terhadap waktu.
Besarnya percepatan sudut dirumuskan sebagai:
Besarnya percepatan sudut dirumuskan sebagai:
Keterangan;
Penentuan kecepatan sudut dari percepatan sudut
Kecepatan sudut dicari melalui percepatan sudut dengan cara mengintegralkan percepatan sudut yang telah diketahui. Secara matematis dapat diuraikan sebagai berikut:
 =
= 
 dω =
dω = 
 dt
dt

 dt
dt
dω =  dt
dt
ωt-ω0 = 
 dt
dt
ωt = ω0 +
Keterangan:
ωt = kecepatan sudut akhir, satuannya rad/s
ω0 = kecepatan sudut awal, satuannya rad/s
 = percepatan sudut, satuannya rad/s2
= percepatan sudut, satuannya rad/s2
t = waktu yang ditempuh, satuannya sekon
ω0 = kecepatan sudut awal, satuannya rad/s
t = waktu yang ditempuh, satuannya sekon
Sedangkan posisi sudut untuk  konstan dicari dengan persamaan:
konstan dicari dengan persamaan:
θt=θ0 + ωt dt
ωt dt
θt=θ0 +
Keterangan:
θ0 = posisi sudut awal, satuannya rad atau putaran
θt = posisi sudut akhir, satuannya rad atau putaran
θt = posisi sudut akhir, satuannya rad atau putaran
Gerakan dengan  yang konstan dinamakan gerak berotasi berubah beraturan.
yang konstan dinamakan gerak berotasi berubah beraturan.
Analogi gerak rotasi dengan gerak translasi
Dari persamaan s = θ r, jika keduanya didifferensialkan terhadap waktu maka akan didapat:
Keterangan:
Keterangan:
v = kecepatan linier, satuannya m/s
ω = kecepatan sudut, satuannya rad/s
r = jari-jari lingkaran, satuannya m
ω = kecepatan sudut, satuannya rad/s
r = jari-jari lingkaran, satuannya m
Vektor kecepatan linier selalu menyinggung lintasan lingkaran. Kecepatan linier disebut kecepatan tangensial dan percepatannnya disebut percepatan tangensial.
Sedangkan hubungan percepatan tangensial dengan percepatan sudut sebagai berikut:



v = ω r
Percepatan sentripetal (as) adalah percepatan yang arahnya selalu menuju ke pusat lingkaran. Persamaannya dinyatakan sebagai:
Percepatan linier total dari partikel yang bergerak melingkar adalah resultan dari kedua komponen percepatan.
Keterangan:
a = percepatan total, satuannya m/s2
at = percepatan tangensial, satuannya m/s2
as = percepatan sentripetal, satuannya m/s2
at = percepatan tangensial, satuannya m/s2
as = percepatan sentripetal, satuannya m/s2
Secara garis besar hubungan antara besaran-besaran dalam gerak rotasi dan gerak translasi dibuat tabel berikut ini:
Contoh Soal
Sepeda motor balap mula-mula diam. Setelah start, 10 sekon kemudian kecepatan rodanya menjadi 36 putaran persekon.
a. Hitungkah percepatan sudut roda sepeda motor
a. Hitungkah percepatan sudut roda sepeda motor
b. Hitunglah jumlah putaran roda selama 10 sekon
Penyelesaian:
Diketahui:
Δ t = 10 sekon
Δ ω = 36 putaran/sekon
Δ t = 10 sekon
Δ ω = 36 putaran/sekon
Soal:
a.  = ... ?
= ... ?
b. θ = .... ?
b. θ = .... ?
Jawab:
a. =
= 
b. θt = θ0 + t2
t2
Momen Gaya
a.
= 
= 3,6.2
= 7,2 rad/s2
rad/s2
= 3,6 put/s2
= 3,6.2
= 7,2
= 3,6 put/s2
b. θt = θ0 +
= 0 +  . 7,2
. 7,2  102
102
= . 720
. 720 
= 360 rad
rad
= 180 putaran
=
= 360
= 180 putaran
Momen Gaya
Dinotasikan dengan  (tau), satuannya N.m.
(tau), satuannya N.m.
Benda dikenakan suatu gaya, salah satu akibatnya adalah terjadinya perubahan gerak pada benda tersebut, yaitu gerak rotasi atau gerak translasi. Hal ini dapat diartikan bahwa bila pada benda dikerjakan gaya, maka akan melakukan gerak rotasi saja atau melakukan rotasi dan translasi atau melakukan gerak translasi saja.
Benda dikenakan suatu gaya, salah satu akibatnya adalah terjadinya perubahan gerak pada benda tersebut, yaitu gerak rotasi atau gerak translasi. Hal ini dapat diartikan bahwa bila pada benda dikerjakan gaya, maka akan melakukan gerak rotasi saja atau melakukan rotasi dan translasi atau melakukan gerak translasi saja.
Sebuah titik O dipengaruhi sebuah gaya F seperti gambar, momen gaya yang timbul dapat dirumuskan sebagai:
Dengan
F = gaya, satuannya N
r = jarak titik O terhadap garis kerja gaya, satuannya meter
Untuk momen gaya karena pengaruh beberapa gaya, maka momen gaya totalnya dapat dihitung dengan menggunakan rumus:
Momen gaya yang mengakibatkan putaran searah jarum jam diberi tanda (+) positif sedangkan momen gaya yang menyebabkan putaran berlawanan dengan jarum jam diberi tanda (-) negatif.
Bila gaya bukan tegak lurus dapat dilakukan dengan
a. mengeser gaya sepanjang garis kerja gaya sehingga tegak lurus dengan posisi sumbu rotasi
b. menguraikan gaya atas komponen-komponennya
Perhatikan animasi berikut ini !
Besarnya momen gaya yang dihasilkan dari gambar adalah
Kopel
Momen kopel dinotasikan dengan M, satuannya N.m.
Kopel adalah pasangan dua buah gaya sama besar berlawanan arah dan sejajar.
Besarnya kopel dinyatakan dengan momen kopel (M). Momen Kopel adalah hasil kali salah satu gaya dengan jarak antara kedua gaya. Momen kopel merupakan besaran vektor dengan satuan N.m. Pengaruh kopel terhadap suatu benda dapat menyebabkan benda berotasi.
Kopel adalah pasangan dua buah gaya sama besar berlawanan arah dan sejajar.
Besarnya kopel dinyatakan dengan momen kopel (M). Momen Kopel adalah hasil kali salah satu gaya dengan jarak antara kedua gaya. Momen kopel merupakan besaran vektor dengan satuan N.m. Pengaruh kopel terhadap suatu benda dapat menyebabkan benda berotasi.
Keterangan:
M = Momen kopel, satuannya N.m
F = Gaya, satuannya newton (N)
d = jarak antara kedua gaya, satuannya meter (m)
F = Gaya, satuannya newton (N)
d = jarak antara kedua gaya, satuannya meter (m)
Contoh penerapan penggunaan kopel dalam kehidupan sehari-hari adalah pada prinsip kerja generator.
Contoh Soal :
Hitung besarnya momen gaya total yang dialami oleh titik B akibat dari pengaruh kedua gaya F1 dan F2!
Jawab :
τ1 = F1 . 2 = 20 . 2 = 40 N.m
τ 2 = F2 . 3 = 10 . 3 = 30 N.m
τ1 = F1 . 2 = 20 . 2 = 40 N.m
τ 2 = F2 . 3 = 10 . 3 = 30 N.m
Momen Gaya totalnya adalah
τ B
= τ 2 – τ 1
= - 10 N.m
Momen Inersia
Momen Inersia Titik Partikel
Dinotasikan dengan I, satuannya kg.m2
Momen inersia suatu partikel adalah hasil kali massa partikel dengan kuadrat jarak terhadap sumbu putarnya dan dirumuskan dengan:
Momen inersia suatu partikel adalah hasil kali massa partikel dengan kuadrat jarak terhadap sumbu putarnya dan dirumuskan dengan:
dimana:
I = momen inersia, satuannya kg.m2
m = massa partikel, satuannya kg
r = jarak partikel terhadap sumbu putar, satuannya m
m = massa partikel, satuannya kg
r = jarak partikel terhadap sumbu putar, satuannya m
Momen Inersia benda tegar
Sebuah elemen massa dm berjarak r terhadap sumbu rotasi. Apabila sebuah benda pejal terdiri dari distribusi materi yang kontinue, maka kita dapat menganggap benda terdiri dari sejumlah besar elemen massa dm yang tersebar merata. Momen Inersia benda adalah jumlah dari momen inersia semua elemen massa tersebut, r2 dm. Untuk dm yang jumlahnya banyak, penjumlahan menjadi sebuah integral.
Dengan batas-batas integral yang dipilih sehingga mencakup seluruh benda.
Besar momen Inersia tergantung pada:
- Bentuk benda
- Massa benda
- Letak sumbu putarnya
Momen Inersia untuk berbagai bentuk benda:
a. Batang Homogen
Dimana:
m = massa batang, satuannya kg
L = panjang batang, satuannya m
m = massa batang, satuannya kg
L = panjang batang, satuannya m
b. Cincin
Keterangan:
m = massa cincin, satuannya kg
R = jari-jari cincin, satuannya m
R = jari-jari cincin, satuannya m
c. Silinder
dengan:
m = massa silinder = kg
R1 = Jari-jari dalam = m
R2 = Jari-jari luar = m
R = Jari-jari silinder berongga atau pejal
R1 = Jari-jari dalam = m
R2 = Jari-jari luar = m
R = Jari-jari silinder berongga atau pejal
d. Bola
- Bola Pejal dengan poros pusat bola
Selanjutnya untuk mencari momen inersia dari benda-benda yang bentuknya seperti di atas tetapi dengan sumbu putar pada jarak L dan sejajar dengan sumbu mula-mula, melalui poros massa, dapat digunakan rumus sumbu sejajar:
dengan
I = Momen Inersia yang baru dalam kg. m2
I0 = momen inersia dengan poros melalui pusat massa dalam kg.m2
M = massa benda dalam kg
L = jarak sumbu mula-mula melalui pusat massa dengan yang baru dalam m
I0 = momen inersia dengan poros melalui pusat massa dalam kg.m2
M = massa benda dalam kg
L = jarak sumbu mula-mula melalui pusat massa dengan yang baru dalam m
Energi Kinetik Rotasi
Energi kinetik rotasi sebuah benda pejal dapat diturunkan dari energi kinetik translasi sebagai berikut:
dengan
m = massa benda dalam kg;
v = kecepatan linier benda dalam m/s2
Ek = energi kinetik benda dalam joule.
v = kecepatan linier benda dalam m/s2
Ek = energi kinetik benda dalam joule.
dengan:
Ek rot = energi kinetik rotasi dalam joule
I = momen inersia benda dalam kg.m2
ω = kecepatan sudut dalam rad/s
I = momen inersia benda dalam kg.m2
ω = kecepatan sudut dalam rad/s
Usaha dalam Gerak Rotasi
Sebuah gaya F bekerja pada jarak R dari sumbu putar benda.
Usaha yang dilakukan oleh sebuah momen gaya  yang bekerja untuk merotasikan sebuah benda tegar sejauh dθ dapat diperoleh dari rumus gerak linier sebagai berikut:
yang bekerja untuk merotasikan sebuah benda tegar sejauh dθ dapat diperoleh dari rumus gerak linier sebagai berikut:
W = F.s = F. Rθ; karena F.R adalah momen gaya maka:
W = F.s = F. Rθ; karena F.R adalah momen gaya maka:
dengan
Dalam gerak rotasi sebuah momen gaya melakukan kerja pada benda dan mengubah energi kinetik rotasinya sesuai dengan hubungan
Pada gerak rotasi juga berlaku hukum kekekalan energi mekanik jika resultan gaya luar sama dengan nol yaitu :
dengan
∆Ep = perubahan energi potensial
∆Ek tran = perubahan energi kinetik translasi
∆Ep = perubahan energi potensial
∆Ek tran = perubahan energi kinetik translasi
∆Ek rot = perubahan energi kinetik rotasi
Hukum Kekekalan Momentum Sudut
Momentum Sudut
Dinotasikan dengan L, satuannya kg.m2/s
Pada gerak rotasi momen inersia I merupakan analogi dari massa m dan ω merupakan analogi dari kecepatan linier v, maka rumus momentum sudut untuk gerak rotasi dapat dituliskan:

 p = m.v dan v = ω.r maka dihasilkan
p = m.v dan v = ω.r maka dihasilkan 
Pada gerak rotasi momen inersia I merupakan analogi dari massa m dan ω merupakan analogi dari kecepatan linier v, maka rumus momentum sudut untuk gerak rotasi dapat dituliskan:
Dengan L = momentum sudut dalam kg. m2/s ; I = momen inersia dalam kg.m2 dan ω = kecepatan sudut dalam rad/s.
Momentum sudut merupakan besaran vektor, maka arah dari momentum sudut dari sebuah benda berotasi adalah seperti berikut:
Hubungan momentum sudut dengan momen gaya
Analogi dengan hubungan impuls dan momentum maka hubungan momentum sudut dengan momen gaya dapat diperoleh :
dengan τ = momen gaya dan dL/dt adalah turunan dari momentum sudut terhadap waktu
Hukum Kekekalan Momentum Sudut
Bila tidak ada gaya dari luar yang bekerja pada benda ( = 0) maka berlaku hukum kekekalan momentum sudut yaitu :
= 0) maka berlaku hukum kekekalan momentum sudut yaitu :
I1 = momen inersia keadaan 1, ω1 = kecepatan sudut keadaan 1, L1 = momentum sudut keadaan 1
I2 = momen inersia keadaan 2, ω2 = kecepatan sudut keadaan 2, L2 = momentum sudut keadaan 2
b. untuk dua benda
I1. ω1 + I2. ω2 = ( I1 + I2 )ω Bila arah gerak searah
I1. ω1 - I2. ω2 = ( I1 + I2 )ω Bila arah gerak berlawanan arah
I1. ω1 - I2. ω2 = ( I1 + I2 )ω Bila arah gerak berlawanan arah
I1 = momen inersia benda 1 dalam kg.m2 ; ω1 = kecepatan sudut benda 1 dalam rad/s
I2 = momen inersia benda 2 dalam kg.m2 ; ω2 = kecepatan sudut benda 2 dalam rad/s
I2 = momen inersia benda 2 dalam kg.m2 ; ω2 = kecepatan sudut benda 2 dalam rad/s
ω = kecepatan sudut benda gabungan benda 1 dan benda 2 dalam rad/s
Gerak Menggelinding
Penerapan dari hukum kekekalan momentum sudut adalah :
- peloncat indah
- penari ballet
Penari ballet berputar perlahan saat membentangkan tangannya. Ketika sang penari melipat tangannya di dada kecepatan putarannya bertambah, dan membentangkan kembali tangannya saat akan berhenti dari putaran. Pada kejadian ini berlaku hukum kekekalan momentum yaitu momentum sudut saat membentangkan sama dengan momentum sudut saat melipat tangannya.
Gerak menggelinding terjadi bila sebuah benda melakukan dua macam gerakan secara bersamaan yaitu gerak translasi dan gerak rotasi.
Contoh gerak menggelinding.
Pada sebuah roda bekerja gaya sebesar F, benda bergerak pada bidang kasar. Dalam hal ini ada dua jenis gerakan, yaitu : gerak translasi dan gerak rotasi.
Pada sebuah roda bekerja gaya sebesar F, benda bergerak pada bidang kasar. Dalam hal ini ada dua jenis gerakan, yaitu : gerak translasi dan gerak rotasi.
Keterangan:
a = percepatan dalam m/s2
fges = gaya gesekan dalam Newton (N)
R = jari-jari roda dalam m
I = momen kelembaman dalam kg.m2
- Gerak translasi berlaku:
ΣF = m.aF – fges = m.a
Keterangan:F = Gaya luar dalam newton (N)
m = massa benda dalam kg
Contoh kasus berikut ini.
Sebuah roda ditarik oleh sebuah gaya sebesar 60 N pada tepi roda (gambar). Roda bergerak mengelinding pada lantai kasar dengan koeffisien gesekan kinetis 0,4. Jika massa roda 5 kg dan jari-jari roda 1 m tentukan besarnya percepatan roda !
Penyelesaian :
Diket : F = 60 N
R = 1 m
m = 5 kg
µ = 0,4
Ditanya : a = …… ?
Diket : F = 60 N
R = 1 m
m = 5 kg
µ = 0,4
Ditanya : a = …… ?
Jawab :
 =
=  .5.12 = 2,5 kg.m2
.5.12 = 2,5 kg.m2
 = I
= I 
 ( F + fges ). R = I
( F + fges ). R = I 

Simulasi